|
|
GeoAstro Applets |
Astronomy |
Chaos Game |
Java |
Miscel- laneous |
Lines
of Daylight Hours Sundial
|
|
Enter latitude in decimal degrees (southern negative), enter longitude in decimal
degrees (western negative), |
|
|
you may use the keys "h", "d", "m", "n" to increase the
hour, date, month, or minute, |
| Hold down the
Control key and click into the applet area to shift
the drawing. Use the "Details" options "Zoom in" or "Zoom out" for scaling. |
| The gnomon (length L)
of this sundial is vertical. The shadow of it's top on
the horizontal plane is used to read the sundial. The declination lines (gray) are computed for full numbers of daylight hours which depend on the latitude of the observer and the declination of the Sun (hour angle H): cos(H) = -
tan(latitude)*tan(declination)
H*15° is
half of the diurnal arc of the Sun on the celestial
sphere (from the local meridian to the horizon).
Example:
latitude 52.52° N, hour angle H=75° means 2*75/15 = 10 hours of daylight By the formula we get the declination -11.23° (occuring on Feb 18 and Oct 22) Select "Data
Window" from the "Details" menu:
For dec1=+23.44° and dec2=-23.44° we get the
maximum and minimum of daylight: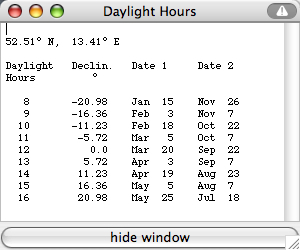 H1 = 124.4° or
2*124.4/15 = 16.6 hours of daylight (summer solstice)
Connecting adjacent intersection points we get
the lines of Italian hours (green lines). Select
"Italian Hours on/off" from the "Details" menu:H2 = 55.6° or 2*55.6/15 = 7.4 hours of daylight (winter solstice) 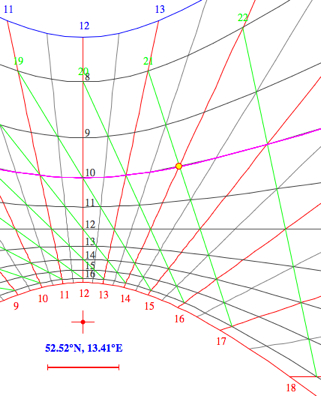 Italian hours begin counting at sunset and end 24 hours later with the following sunset. Example: Standard Time 14:21 on Feb 19 (14:01 local time) is 3 hours before sunset (at 17:21 Standard Time), i.e. 21:00 in Italian hours, 3 hours before sunset. In this applet the times of sunrise and sunset are for h=0° altitude (discarding atmospheric refraction) instead of -0.83°. For low and mid latitudes the difference is only a few minutes. sin h =
sin(lat) sin(dec) + cos(lat) cos(dec)
cos(H)
Setting the
altitude to h=0:
H = arc cos[-tan(lat) tan(dec)] |
More of my applets:
Babylonian, Italian and Unequal Hours Applet
Planetary (Unequal) Hours Clock
More of my sundial applets ...
|
|
Updated:
2023, Oct 12
©
2010-2023 J. Giesen
![]()

