Ancient Models of the Sun's Motion: Epicyclic Model Applet

Home

Site Map

GeoAstro
Applets

Astronomy

Chaos Game

Java

Miscel-
laneous

Ancient Theories of the Sun:
2. Epicyclic Model Applet

1. Eccentric Model Applet

3. Eccentric and Equant Model Applet

data

Select from the Details menu.

time
interval
Select the time interval.

year
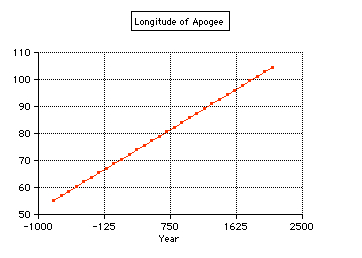
The angular position of the apogee of the Sun is slowly moving with time (about 1.71° per cencury, this is not the precession of the equinoxes).

longitude
Determination of the Earth's Orbital Parameters (NASA)

Eccentric Model Applet

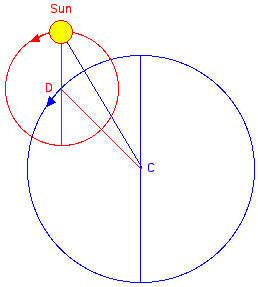
There are two mathematically equivalent models of ancient Greek astronomy explaining the unequal motion of the Sun:

epicycle
sun

eccentric
sun

The Sun moving on the epicycle with center D rotating on the deferent circle (center C) at the same angular speed.
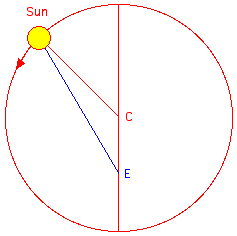
The Sun moving on the circle (radius r) centered at C seen from the eccentric point E.
(eccentricity e = CE/r)

Lenghts of the seasons:

Hipparchus (90 BC-120 BC)
Ptolemy (90 AD-168 AD)
applet
100 BC
Meeus
0
Meeus
2000

Spring vernal equinox
-
summer solstice
94 1/2 d
94.51 d 93.96 d 92.76 d

Summer summer solstice
-
autumnal equinox
92 1/2 d 92.55 d 92.45 d
93.65 d

Autumn autumnal equinox
-
winter solstice
88 1/8 d 88.11 d 88.69 d
89.84 d

Winter winter solstice
-
vernal equinox
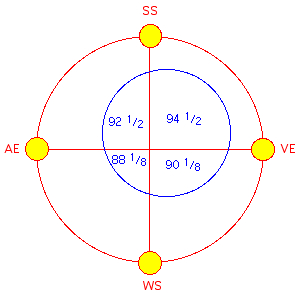
90 1/8 d 90.07 d 90.13 d
88.99 d

Sum
365 1/4 d
365.24 d 365.23 d 365.24 d

seasons

data

Rounded number of days in zodiac signs:

	Ari	Tau	Gem	Can	Leo	Vir	Lib	Sco	Sag	Cap	Aqu	Pis
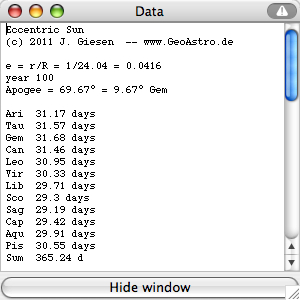
days	31	32	32	31	31	30	30	29	29	29	30	31	365
days	95			92			88			90			365

Seasons Applet

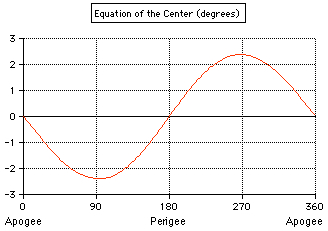
equation of the center

The equation of the center (EoC) is the difference between the actual position of the Sun and the position it would have if its angular motion were uniform.
From apogee to perigee the actual Sun is behind the mean Sun (EoC negative), from perigee to apogee the apparent Sun is in advance (EoC positive).
The maximum value of the equation of the center is at 90° from apogee:

maxEoC = arcsin(e)

e=1/24.0    maxEoC = 2° 23.3'
e=1/24.1    maxEoC = 2° 22.7'
e=1/24.04    maxEoC = 2° 23.0'

Ptolemy:
e=1/24.04 maxEoC = 2° 23'

In the appendix 2 "Calculation of the Eccentric-Quotient for the Sun" of Thurston's book, e is computed to be 143/3438 = 24.04, using the lengths of the seasons and 365 d ¹⁴/₆₀ h ⁴⁸/₃₆₀₀ min = 365.2467 d for the length of the tropical year given by Ptolemy.

Web Links

Hipparchus: Orbit of the Sun (Wikipedia)

Ptolemy (Wikipedia)

Jahreszeit (Wikipedia)

Gemini Elementa Astronomiae, editit C. Manitius (PDF, Greek/German)

Des Claudius Ptolemäus Handbuch der Astronomie (Übers. Karl Manitius)

Books

James Evans: The History and Prctice of Ancient Astronomy,
Oxford University Press, 1998, Chapter Five: Solar Theory.

Hugh Thurston: Early Astronomy, Springer, Berlin/New York 1994.

Jean Meeus: Astronomical Tables of the Sun, Moon and Planets. 2nd ed., Willmann-Bell, Richmond 1995.

Updated: 2023, Oct 07

	Select from the Details menu.
	Select the time interval.
	The angular position of the apogee of the Sun is slowly moving with time (about 1.71° per cencury, this is not the precession of the equinoxes). Determination of the Earth's Orbital Parameters (NASA)

There are two mathematically equivalent models of ancient Greek astronomy explaining the unequal motion of the Sun:

The Sun moving on the epicycle with center D rotating on the deferent circle (center C) at the same angular speed.	The Sun moving on the circle (radius r) centered at C seen from the eccentric point E. (eccentricity e = CE/r)

		Hipparchus (90 BC-120 BC) Ptolemy (90 AD-168 AD)	applet 100 BC	Meeus 0	Meeus 2000
Spring	vernal equinox - summer solstice	94 1/2 d	94.51 d	93.96 d	92.76 d
Summer	summer solstice - autumnal equinox	92 1/2 d	92.55 d	92.45 d	93.65 d
Autumn	autumnal equinox - winter solstice	88 1/8 d	88.11 d	88.69 d	89.84 d
Winter	winter solstice - vernal equinox	90 1/8 d	90.07 d	90.13 d	88.99 d
Sum		365 1/4 d	365.24 d	365.23 d	365.24 d