|
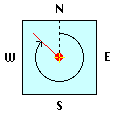
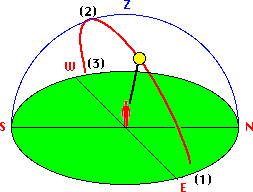
The observer is located at the centre of his "celestial sphere" with zenith Z above his head and
the horizon plane N-E-S-W.
The Sun rises at (1), moves along the red arc,
passing the meridian NZS at (2), and sets at (3).
This path is called the diurnal arc of the sun.
Projecting the diurnal arc (circle of
declination) of the Sun and the horizontal plane
into the NZS plane, they are seen as straight lines
intersecting at (1)=(3).
The diurnal arc (declination circle) of the
sun varies with the seasons:
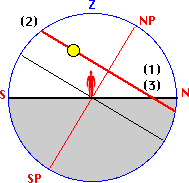 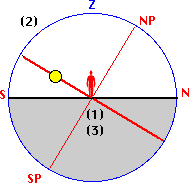
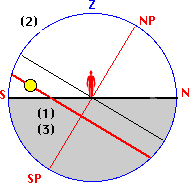
Summer Solstice
|
Equinox |
Winter Solstice
|
There are two
reasons for the difference between the standard
time and the solar time. To convert solar time to
standard time:
- add 4 minutes per degree west of the time zone
meridean, and subtract if east, and take into
account daylight saving time. For Berlin - time
zone meridian 15° E and longitude 13.41° E, add
1.59*4 min = 6.4 minutes.
- subtract the equation of time, due to the
elliptic orbit of the earth around the Sun and
the obliquity of the ecliptic (23.44°).
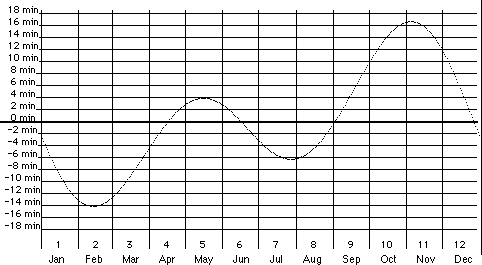
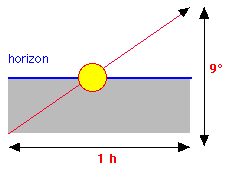
The moment of sunrise is usually defined by
the instant when the center of the sun is -0.83°
below horizon (taking into account the refraction of
light by the atmosphere of the earth and the
apparent diameter of the Sun). For a latitude of 50°
this equivalent to a time interval of 5 to 7
minutes.
As shown below the construction is in
agreement with the equation known from spheric
trigonometry:
(1) sin h = sin φ
sin δ + cos
φ cos δ cos τ
(2) cos Az = (sin δ - sin φ sin h)/(cos h cos φ)
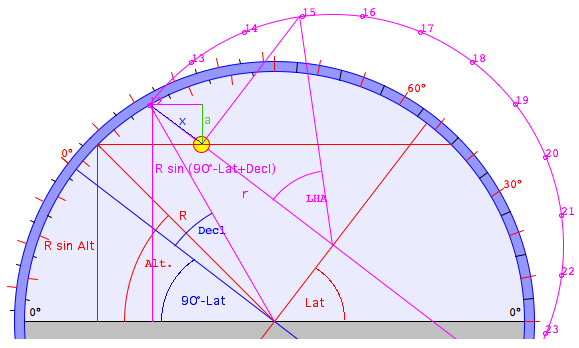
φ
= Latitude, h = Altitude, δ = Declination, τ =
Local Hour Angle LHA
(1) We
start computing a, the difference between the
vertical lines
a = R sin (90°-φ+δ) - R sin h
a = x sin (90°-φ) = x cos φ
x = r - r cos
τ =
r (1-cos τ)
r = R cos δ
a = R
cos
δ
(1-cos
τ)
cos φ
sin (90°-φ+δ) = sin (90°-φ) cos δ
+ cos (90°-φ) sin δ = cos φ cos δ + sin φ
sin δ
sin h = cos φ cos δ + sin φ
sin δ - cos δ (1-cos τ) cos φ
sin h = sin φ sin δ + cos φ cos δ cos τ
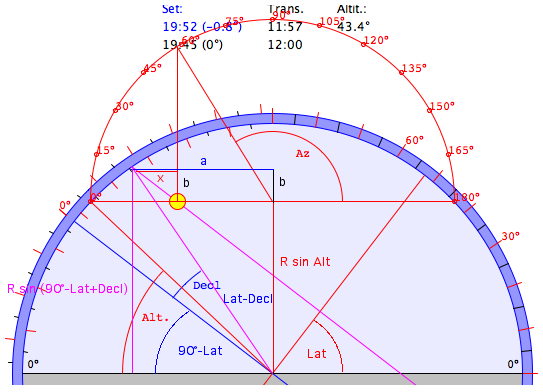
φ
= Latitude, h = Altitude, δ = Declination, τ =
Local Hour Angle LHA
(2) We
start computing b, the difference between
the vertical lines
b = R
sin (90°-φ+δ) - R sin h = x tan (90°-φ)
x = a
- r cos (180°-az)
cos (180°-az) = - cos az
a = R sin (φ-δ)
r = R cos h
x = R sin (φ-δ) +
R cos h cos az
R sin
(90°-φ+δ) - R sin h = [R
sin (φ-δ) + R cos h cos az] tan (90°-φ)
sin (90°-φ+δ) - sin h = (sin (φ-δ) +
cos h
cos az) tan (90°-φ)
sin (90°-φ+δ) - sin h = sin (φ-δ) + cos h cos
az] cos φ/sin
φ
cos φ cos δ
+ sin φ sin δ - sin
h = [sin φ cos δ
- cos φ sin δ + cos h cos az]
cos φ/sin
φ
sin φ
cos φ
cos δ + sin2
φ
sin δ - sin φ
sin h = [sin φ
cos δ - cos φ
sin δ + cos
h
cos az]
cos φ
sin φ
cos φ
cos δ
+ sin2 φ
sin δ - sin φ
sin h
= cos φ
sin φ
cos δ - cos2 φ sin δ + cos φ
cos
h
cos az
sin2
φ
sin δ - sin
φ
sin h = -
cos2 φ sin δ + cos φ
cos
h
cos az
sin
δ
- sin
φ
sin
h = cos φ
cos
h
cos az
sin
δ
- sin
φ
sin
h =
cos φ
cos
h
cos az
cos Az =
(sin δ - sin φ sin
h)/(cos h cos φ)
Both
equations (1 and 2) can also
be found within the
construction of my applet Quadratum
Horarium Generale
(Regiomontanus Dial).
|